Сферы и прямые
Существует три возможных относительных положения для сферы и прямой в пространстве.
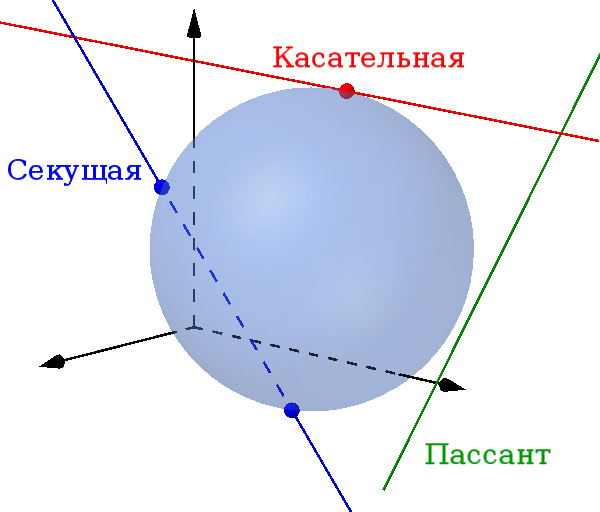
Запомните
- Пассант - это прямая линия, не имеющая ничего общего со сферой.
- Касательная имеет ровно одну общую точку.
- Секущая имеет две общие точки со сферой.
Таким образом, сфера и прямая могут иметь одну, две или не иметь общей точки.
Отдельные координаты используются в уравнении сферы для вычисления точек пересечения.
Метод
- Запишите координаты $g$
- Вставьте и решите уравнения в уравнении сферы
- Вставьте $r$ в прямую, чтобы получить пересечение(я)
Например
$g: \vec{x} = \begin{pmatrix} 5 \\ 6 \\ 5 \end{pmatrix} + r \cdot \begin{pmatrix} 3 \\ 2 \\ 2 \end{pmatrix}$
$k: (x+1)^2+(y-2)^2$ $+(z-1)^2=17$
-
Разбейте $g$ на 3 уравнения
Мы заменяем $\vec{x}$ и записываем соответствующие координаты, как собственное уравнение.
$\begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 5 \\ 6 \\ 5 \end{pmatrix} + r \cdot \begin{pmatrix} 3 \\ 2 \\ 2 \end{pmatrix}$
- $x=5+3r$
- $y=6+2r$
- $z=5+2r$
-
Вставьте координаты
Теперь эти уравнения используются в уравнении сферы для $x$, $y$ и $z$.
$(x+1)^2+(y-2)^2$ $+(z-1)^2=17$
$(5+3r+1)^2$ $+(6+2r-2)^2$ $+(5+2r-1)^2=17$
$(6+3r)^2$ $+(4+2r)^2$ $+(4+2r)^2=17$
Используйте биномиальную теорему для раскрытия скобок
$36+36r+9r^2$ $+16+16r+4r^2$ $+16+16r+4r^2=17$
$17r^2+68r+68=17\quad|-17$
$17r^2+68r+51=0\quad|:17$
$r^2+4r+3=0$
Используйте формулу корней квадратного уравнения I для решения квадратного уравнения.
$r_{1,2}=-\frac{p}2\pm\sqrt{(\frac{p}2)^2-q}$
$r_{1,2}=-2\pm\sqrt{2^2-3}$
$r_{1,2}=-2\pm1$$r_{1}=-1$ и $r_{2}=-3$
-
Вставьте $r$
Два вычисленных $r$ вставляются в уравнение прямой, чтобы получить точки пересечения.
$\vec{OS_1} = \begin{pmatrix} 5 \\ 6 \\ 5 \end{pmatrix} - 1 \cdot \begin{pmatrix} 3 \\ 2 \\ 2 \end{pmatrix}$ $=\begin{pmatrix} 2 \\ 4 \\ 3 \end{pmatrix}$
$\vec{OS_2} = \begin{pmatrix} 5 \\ 6 \\ 5 \end{pmatrix} - 3 \cdot \begin{pmatrix} 3 \\ 2 \\ 2 \end{pmatrix}$ $=\begin{pmatrix} -4 \\ 0 \\ -1 \end{pmatrix}$
Это секущая, которая пересекает сферу в точке $S_1(2|4|3)$ и $S_2(-4|0|-1)$.
