Естественная показательная функция

Особым видом показательных функций, является естественная показательная функция или экспоненциальная функция с основанием e .

$f(x)=e^x$

Вывод

Производная от экспоненциальной функции, смещается вправо или влево .

Например: $f(x)=2^x$

Теперь можно попытаться сделать расстояние сдвинутой производной еще меньше. Таким образом, должна быть одна производная, расстояние которой равно нулю и поэтому соответствует функции.

Леонард Эйлер (1707-1783) нашел именно эту экспоненциальную функцию, которая не сдвигается при выводе и тем самым дает изначальную функцию.

$f(x)=e^x=f'(x)$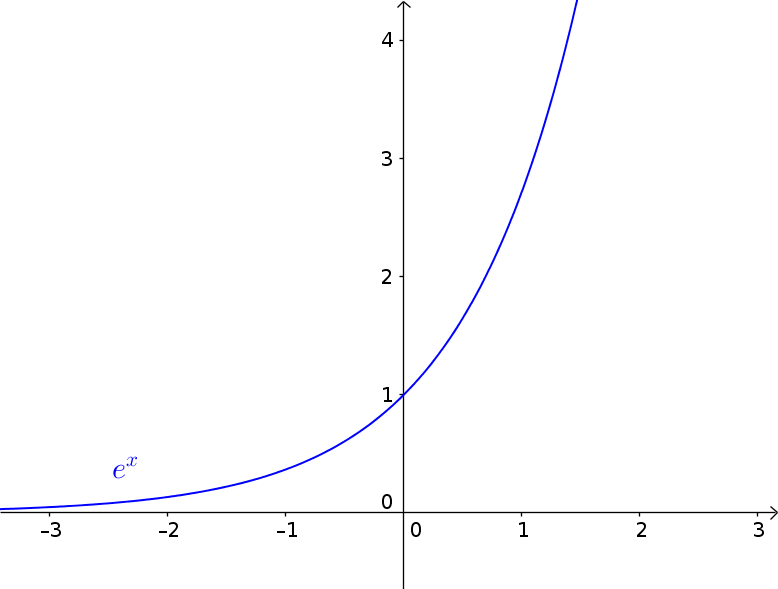

Запомните

Естественная показательная функция - это экспоненциальная функция с числом Эйлера в качестве базы.

Полученный результат и идентичная функция:
$f(x)=e^x$
$f'(x)=e^x$

Подсказка

Число Эйлера $e$ как $\pi$, является постоянным иррациональным числом. Это $e = 2,7182818...$.