Производные показательных функций
При вычислении производной от общих показательных функций используется : натуральный логарифм.
!
Запомните
$f(x)=a^x$
$f'(x)=a^x\cdot\ln(a)$
$f'(x)=a^x\cdot\ln(a)$
Например
$f(x)=2^x$
$f'(x)=2^x\cdot\ln(2)$
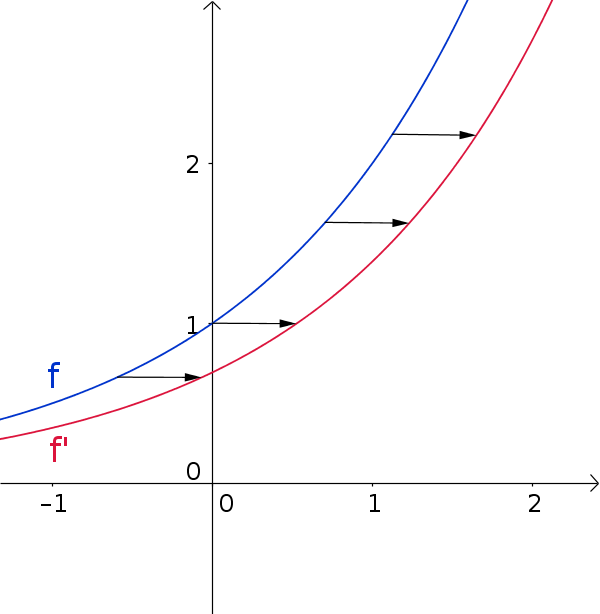
При вычислении производной показательной функции она смещается вдоль оси x.
Вывод
Здесь описывается нахождение производной.
Мы ищем производную от $f(x)=a^x$
Перепишите как показательную функцию
Поскольку ln-функция является обратной экспоненциальной функцией, то применяется следующее:
$x=e^{\ln(x)}$
$a^x=e^{\ln(a^x)}$Теперь, закон логарифмов применяется для степеней.
$f(x)=a^x=e^{x\cdot\ln(a)}$
$a^x=e^{x\cdot\ln(a)}$Вычислите производную от показательной функции
$f(x)=e^{g(x)}$
$f'(x)=e^{g(x)}\cdot g'(x)$
$f(x)=e^{x\cdot\ln(a)}$
$f'(x)=e^{x\cdot\ln(a)}\cdot(x\cdot\ln(a))'$$\ln(a)$является постоянным коэфициентом ( (правило постоянного коэфициента ) и $(x)'=1$
$f'(x)=e^{x\cdot\ln(a)}\cdot\ln(a)$Перепишите показательную функцию
Примените решение с первого шага :
$a^x=e^{x\cdot\ln(a)}$
$f'(x)=e^{x\cdot\ln(a)}\cdot\ln(a)$
$f'(x)=a^x\cdot\ln(a)$
