Exponentielle Zu- und Abnahme
Exponentielles Wachstum bezeichnet sowohl die exponentielle Zu- als auch Abnahme.
Es gilt die Formel:
$N(t)=N_{0}\cdot a^t$
!
Merke
Zu- oder Abnahme lässt sich anhand vom Wachstumsfaktor $a$ unterscheiden:
- Wenn $a>1$, liegt exponentielle Zunahme vor.
- Wenn $0 < a < 1$, liegt exponentielle Abnahme vor.
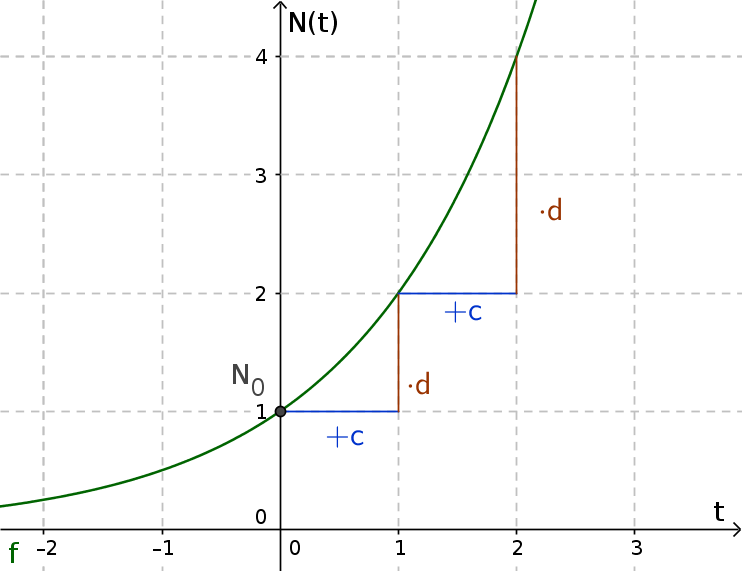
Exponentielle Zunahme
Bei exponentieller Zunahme ist der Wachstumsfaktor immer größer als 1. Man erhält also mehr als man vorher hatte.
Beispiele
- $N(t)=2\cdot3^t$
- $N(t)=50\cdot(\frac54)^t$
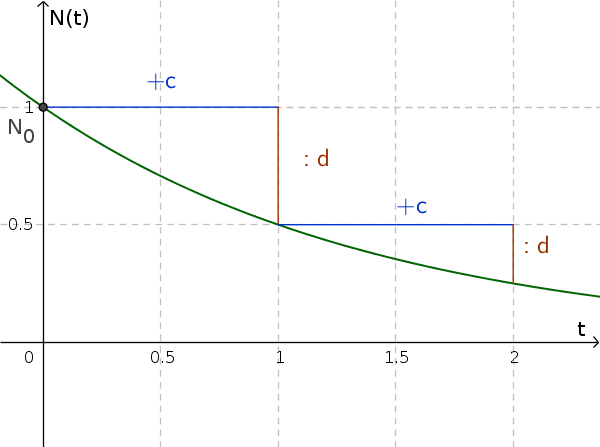
Exponentielle Abnahme
Bei exponentieller Abnahme ist der Wachstumsfaktor immer kleiner als 1 (und größer als 0). Der Bestand verringert sich also mit zunehmendem $t$.
Da wir einen Bruch, z. B. $\frac1d$ als Wachstumsfaktor haben, können wir uns dies auch als Division vorstellen.
Beispiele
- $N(t)=10\cdot(\frac13)^t$
- $N(t)=\frac12\cdot(\frac78)^t$
- $N(t)=3\cdot(0,25)^t$
i
Tipp
Beachte, dass die Regel nur mit positivem $t$ gilt. Negative Exponenten lassen sich hingegen umschreiben:
$N(t)=N_0\cdot b^{-t}$ $=N_0\cdot (\frac1b)^t$
In diesem Fall, wenden wir die Regel oben für $a=\frac1b$ an.Beispiele
- $N(t)=2^{-t}=(\frac12)^t$ ⇒exponentielle Abnahme
- $N(t)=(\frac13)^{-t}=3^t$ ⇒exponentielle Zunahme
